6. 統計的仮説検定

関心のある仮説が正しいか否かをデータから判定する統計手法が仮説検定である．仮説検定のポイントは，否定することに高い信頼性を持たせたい主張を帰無仮説に設けることである．帰無仮説を否定することに99%(有意水準1%)や95%(有意水準5%)の信頼性を持たせることによって，強い主張(帰無仮説)を保証することが仮説検定の考え方である．

6.1 仮説検定の考え方

仮説検定(Statistical test)とは，母集団の特性(値)を定量的に求めようとする「推定」や「予測(回帰)」とは異なり，母集団の特性に対する仮説が正しいことを，「支持する(真, 仮説を受容) or 支持しない(偽, 仮説を棄却)」の二者択一で判定するための方法論です．しかるに，有意水準$\alpha$や$P$値といった指標は，この二者択一の判断に対して妥当性（信頼性）を保証するための数値でしかありません．

どんな検定方式を使おうが，仮説検定の枠組みに入る統計手法である限り，実際の観測データから得られる結果は，仮説を支持する/支持しないのいずれかであることに注意してください．仮説検定は観測データに対する仮説そのものの妥当性を定量的に見積もることはできません．

仮説検定(Statistical test)の定義

仮説(Hypothesis)

母集団に対する何らかの記述．「母数$\theta$に対する仮説」の場合，母数$\theta$が母数空間$\Theta$を分割する2つの背反する部分集合$\Theta_0, \Theta_1$のどちらかに属するかを記述する．
- 帰無仮説(Null hypothesis) $H_0: \theta \in \Theta_0$ 「母数$\theta$が$\Theta_0$に属する」
- 対立仮説(Alternative hypothesis) $H_1: \theta \in \Theta_1$ 「母数$\theta$が$\Theta_1$に属する」
検定(Testing)

標本$X \in \mathcal{X}$から求める検定統計量(Test statistics) $T(X)$を用いて行う，帰無仮説$H_0$が「真か偽か」の判定．
- 受容(Accept) 「帰無仮説$H_0$が真である」と検定すること
- 棄却(Reject) 「帰無仮説$H_0$が偽である」と検定すること

ここで以下に注意してください，

「仮説」は母数空間$\Theta$に対する記述である
「検定」は標本空間$\mathcal{X}$に基づく判定である

　さて，次に問題となるのは，「母集団に対する何らかの仮説$H_0$が与えられたとき、それをどのように「真 / 偽」と判定するか？」，言い換えると「ある仮説が与えられたとき、それをどのように検定するのか？」です。このような「検定を実施する方法」のことを，検定方式と言います．

　ある仮説に対する統計的仮説検定そのものの「性質」は、検定を行う方式（＝検定方式）によって決まります．１つの仮説（: 例えば「母集団の平均は1である」）に対して，「支持する or 支持しない」の判断を下す方法として、複数の検定方式が考えられます．

棄却域と有意水準

(帰無仮説$H_0$の)棄却域 $R$
- 標本$X := \{X_1, \dots, X_n\}$と，標本に対して定まる検定統計量$T(X)$を用いて以下のように定義される．
  \[\begin{align} R &= \left\{ x \in X ~\vert~ \text{帰無仮説}H_0\text{が棄却されるための標本統計量}T(X)\text{の条件} \right\} \\ \nonumber &= \left\{ x \in X ~\vert~ T(X) \leq C \right\} \nonumber \end{align}\]
(帰無仮説$H_0$の)受容域 $A$

標本$X := \{X_1, \dots, X_n\}$と，標本に対して定まる検定統計量$T(X)$を用いて以下のように定義される．
\[\begin{align} A &= \left\{ x \in X ~\vert~ \text{帰無仮説}H_0\text{が受容されるための標本統計量}T(X)\text{の条件} \right\} \\ \nonumber &= \left\{ x \in X ~\vert~ T(X) \gt C \right\} \nonumber \end{align}\]

標本$X := \{X_1, \dots, X_n\}$は（ある確率分布に従う）母集団から抽出されたものだから，「標本$X$が帰無仮説$H_0$の棄却域$R$に属する確率」を考えることができます．さらに，$R,A$の定義から，これらは標本$X$に対する検定統計量$T(X)$によって測ることができます．

\[P(X \in R) = P(T(X) \leq C) \\ P(X \in A) = P(T(X) \gt C)\]

このとき，有意水準(Significance lebel) $\alpha$ を定義します．

有意水準$\alpha$の検定

「標本$X$に基づいて，帰無仮説$H_0: \theta \in \Theta_0$を棄却する」という判断が間違っている確率が，大きくても$\alpha$以下であるような検定．すなわち，以下を満たすような検定のこと.

\[\sup_{\theta \in \Theta_0} P(X \in R) = \sup_{\theta \in \Theta_0} P(T(X) \leq C) \leq\alpha\]

有意水準$\alpha$の値としては，通常$\alpha=0.05, \alpha=0.01$が用いられます．

例: 帰無仮説$H_0$と棄却域$R$

ある地域の中学生の平均身長$\mu$が，全国平均$\mu_0$に等しいかを検定するケースを考える．$n$人の標本$X = \{X_1, \dots, X_n\}$が得られた場合，仮説検定は，

帰無仮説$H_0: \mu = \mu_0$ 「ある地域の平均身長$\mu$が，全国平均$\mu_0$に等しい」
対立仮説$H_1: \mu \neq \mu_0$ 「ある地域の平均身長$\mu$が，全国平均$\mu_0$に等しくない」

であり，定数$C$を用意して，

「$\vert \bar{X} - \mu_0 \vert \gt C$」ならば$H_0$を棄却．（$H_1$を受容）
「$\vert \bar{X} - \mu_0 \vert \leq C$」ならば$H_0$を受容．（$H_1$を棄却）

とするのが自然である．このとき，検定統計量は$T(X) := \vert \bar{X} - \mu_0 \vert$と定義できるから．これを用いて，

帰無仮説$H_0$の棄却域$R = \left\{ x \in X ~\vert~ T(X) \gt C \right\}$
帰無仮説$H_0$の受容域$A = \left\{ x \in X ~\vert~ T(X) \leq C \right\}$

が定まる．さらに，統計量$T(X)$の標本分布が分かっていれば，

確率 $P(X \in R) = P(T(X) \gt C)$
確率 $P(X \in A) = P(T(X) \leq C)$

が計算できるから，有意水準$\alpha$を元に，仮説$H_0$の棄却/受容を判定できる．

有意(Significance)

有意(Significance)は統計学の用語で，「確率的に偶然とは考えにくく，必然的であると考えられる」ことを指します．

有意確率(P値)

母集団に従う標本$X = \{X_1, \dots, X_n\}$と，その実現値$x := \{x_1, \dots, x_n \}$を考えます．このとき，「帰無仮説$H_0: \theta \in \Theta_0$の下で測られる，検定統計量$T(X)$に対してその実現値$T(x)$が逸脱している最大確率$p(x)$」を有意確率（p値, p value）といいます．

\[p(x) := \sup_{\theta \in \Theta_0} P(T(X) \leq T(x))\]

p値は，$T(X)$の確率分布に依存する確率変数です．

また，有意水準$\alpha$の定義から，定数$C = T(x)$とすれば，有意水準$\alpha$と$p$値の同等性が導かれます．

\[\begin{align} \text{有意水準}\alpha\text{の検定} &\Leftrightarrow \sup_{\theta \in \Theta_0} P(T(X) \leq T(x)) \leq \alpha \nonumber \\ &\Leftrightarrow p(x) \leq \alpha \nonumber \\ &\Leftrightarrow p\text{値が有意水準}\alpha\text{以下である．} \end{align}\]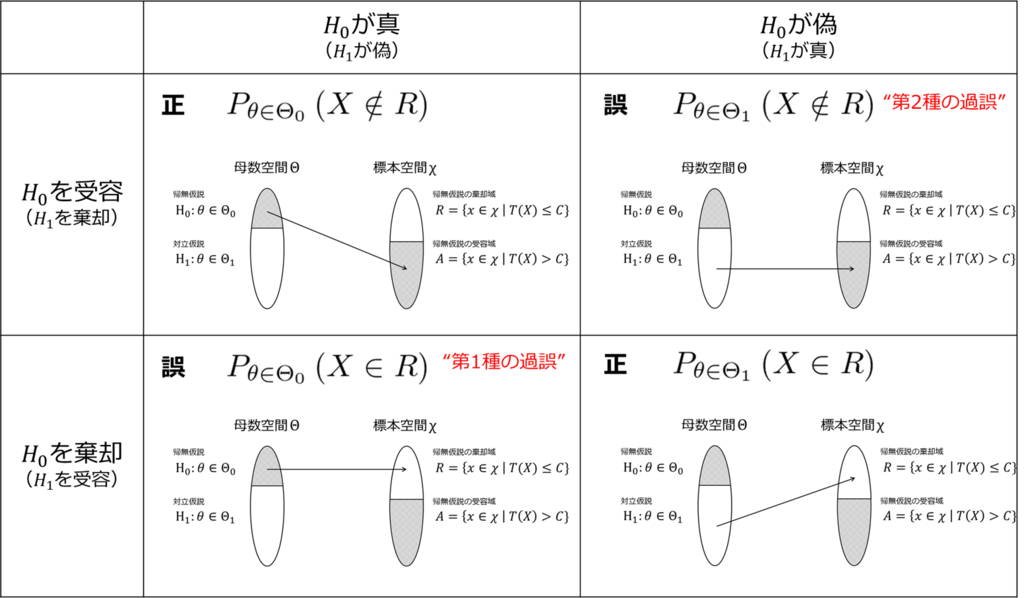

6.2 正規母集団についての仮説検定

正規分布$\mathcal{N}(\mu, \sigma^2)$に従う母集団を正規母集団といいます．手元にある標本(観測データ)に対して，母分布に正規分布を仮定して行う仮説検定として代表的なものを紹介します．

A. 1標本の正規母集団
- A1: 母平均$\mu$の検定（母分散$\sigma^2$が既知）
- A2: 母平均$\mu$の検定（母分散$\sigma^2$が未知）　”t検定”
- A3: 母分散$\sigma^2$の検定
B. 2標本の正規母集団（母分散$\sigma^2_1, \sigma^2_2$が等しい）
- B1: 母平均$\mu_1, \mu_2$の同等性の検定（母分散$\sigma^2_1, \sigma^2_2$が既知）
- B2: 母平均$\mu_1, \mu_2$の同等性の検定（母分散$\sigma^2_1, \sigma^2_2$が未知）　”t検定”
C. 2標本の正規母集団（母分散$\sigma^2_1, \sigma^2_2$が等しくない）
- C1: 母平均$\mu_1, \mu_2$の同等性の検定（母分散$\sigma^2_1, \sigma^2_2$が既知）
- C2: 母平均$\mu_1, \mu_2$の同等性の検定（母分散$\sigma^2_1, \sigma^2_2$が未知）
- C3: 母分散$\sigma^2_1, \sigma^2_2$の同等性の検定　”F検定”

A. 1標本の正規母集団

A1: 母平均$\mu$の検定（母分散$\sigma^2$が既知）

両側検定の帰無仮説$H_0: \mu = \mu_0$の下で，中心極限定理より，

\[\frac{\bar{X} - \mu_0}{\sqrt{\frac{\sigma^2}{n}}} \underset{d}{\to} \mathcal{N}(0, 1)\]

だから，帰無仮説$H_0: \mu = \mu_0$の有意水準$\alpha$の棄却域は次式．

\[R = \left\{ X \in \mathcal{X} ~\vert~ \sqrt{n} \frac{\bar{X} - \mu_0}{\sigma} \gt Z_{\frac{\alpha}{2}} \right\}\]

A2: 母平均$\mu$の検定（母分散$\sigma^2$が未知）　”t検定”

両側検定の帰無仮説$H_0: \mu = \mu_0$の下で，

\[\frac{\bar{X} - \mu_0}{\sqrt{\frac{V^2}{n}}} \underset{d}{\to} t_{n-1}\]

だから，帰無仮説$H_0: \mu = \mu_0$の有意水準$\alpha$の棄却域は次式．

\[R = \left\{ X \in \mathcal{X} ~\vert~ \sqrt{n} \frac{\bar{X} - \mu_0}{V} \gt t_{n-1, \frac{\alpha}{2}} \right\}\]

A3: 母分散$\sigma^2$の検定

両側検定の帰無仮説$H_0: V^2 = \sigma^2_0$の下で，

\[\frac{(n-1)V^2}{\sigma^2_0} \sim \chi^2_{n-1}\]

だから，帰無仮説$H_0: V^2 = \sigma^2_0$の有意水準$\alpha$の棄却域は次式．

\[R = \left\{ X \in \mathcal{X} ~\vert~ \frac{(n-1)V^2}{\sigma^2_0} \lt \chi^2_{n-1, 1-\frac{\alpha}{2}} ~or~ \chi^2_{n-1, 1-\frac{\alpha}{2}} \lt \frac{(n-1)V^2}{\sigma^2_0} \right\}\]

B. 2標本の正規母集団（母分散$\sigma^2$が等しい）

B1: 母平均$\mu_1, \mu_2$の同等性の検定（母分散$\sigma^2_1, \sigma^2_2$が既知）

両側検定の帰無仮説$H_0: \mu_X = \mu_Y$の下で，中心極限定理より，

\[\frac{\bar{X} - \bar{Y}}{\sqrt{\frac{m+n}{mn} \sigma^2}} \underset{d}{\to} \mathcal{N}(0,1)\]

だから，帰無仮説$H_0: \mu_X = \mu_Y$の有意水準$\alpha$の棄却域は次式．

\[R = \left\{ X \in \mathcal{X} ~\vert~ \sqrt{\frac{mn}{m+n}} \frac{\vert \bar{X} - \bar{Y} \vert}{\sigma} \gt Z_{\frac{\alpha}{2}}\right\}\]

B2: 母平均$\mu_1, \mu_2$の同等性の検定（母分散$\sigma^2_1, \sigma^2_2$が未知）　”t検定”

（2標本に共通する）母分散の推定量$\hat{\sigma}^2$を以下のように定義する．

\[\hat{\sigma^2} := \frac{1}{m+n-2} \left\{ \sum_{i=1}^{m} {(X_i - \bar{X})}^2 + \sum_{j=1}^{n} {(Y_i - \bar{Y})}^2 \right\}\]

両側検定の帰無仮説$H_0: \mu_X = \mu_Y$の下で，

\[\frac{\bar{X} - \bar{Y}}{\sqrt{\frac{m+n}{mn} \hat{\sigma}^2}} \sim t_{m+n-2}\]

だから，帰無仮説$H_0: \mu_X = \mu_Y$の有意水準$\alpha$の棄却域は次式．

\[R = \left\{ X \in \mathcal{X} ~\vert~ \sqrt{\frac{mn}{m+n}} \frac{\vert \bar{X} - \bar{Y} \vert}{\hat{\sigma}} \gt t_{m+n-2, \frac{\alpha}{2}}\right\}\]

C. 2標本の正規母集団（母分散$\sigma^2$が等しくない）

C1: 母平均$\mu_1, \mu_2$の同等性の検定（母分散$\sigma^2_1, \sigma^2_2$が既知）

両側検定の帰無仮説$H_0: \mu_X = \mu_Y$の下で，中心極限定理より，

\[\frac{\bar{X} - \bar{Y}}{\sqrt{\frac{\sigma_X^2}{m} + \frac{\sigma_Y^2}{n}}} \underset{d}{\to} \mathcal{N}(0,1)\]

だから，帰無仮説$H_0: \mu_X = \mu_Y$の有意水準$\alpha$の棄却域は次式．

\[R = \left\{ X \in \mathcal{X} ~\vert~ \frac{\bar{X} - \bar{Y}}{\sqrt{\frac{\sigma_X^2}{m} + \frac{\sigma_Y^2}{n}}} \gt Z_{\frac{\alpha}{2}}\right\}\]

C2: 母平均$\mu_1, \mu_2$の同等性の検定（母分散$\sigma^2_1, \sigma^2_2$が未知）

両側検定の帰無仮説$H_0: \mu_X = \mu_Y$の下で，ウェルチの検定(Welch’s test)より，

\[\frac{\bar{X} - \bar{Y}}{\sqrt{\frac{V_X^2}{m} + \frac{V_Y^2}{n}}} \underset{\text{近似分布}}{\to} t_{f}\]

ただし，t分布の自由度$f$は次の値．

\[f := \frac{ { \left( \frac{V_X^2}{m} + \frac{V_Y^2}{n}\right) }^2 }{ \frac{V_X^2}{m(m-1)} + \frac{V_Y^2}{n(n-1)} }\]

だから，帰無仮説$H_0: \mu_X = \mu_Y$の有意水準$\alpha$の棄却域は次式．

\[R = \left\{ X \in \mathcal{X} ~\vert~ \frac{\bar{X} - \bar{Y}}{\sqrt{\frac{V_X^2}{m} + \frac{V_Y^2}{n}}} \gt t_{f, \frac{\alpha}{2}}\right\}\]

C3: 母分散$\sigma^2_1, \sigma^2_2$の同等性の検定　”F検定”

両側検定の帰無仮説$H_0: \sigma_X^2 = \sigma_Y^2$の下で，

\[\frac{V_X^2 / \sigma_X^2}{V_Y^2 / \sigma_Y^2} = \frac{V_X^2}{V_Y^2} \sim F_{m-1, n-1}\]

だから，帰無仮説$H_0: \sigma_X^2 = \sigma_Y^2$の有意水準$\alpha$の棄却域は次式．

\[R = \left\{ X \in \mathcal{X} ~\vert~ \frac{V_X^2}{V_Y^2} \lt F_{m-1,n-1, 1-\frac{\alpha }{2}} ~or~ F_{m-1,n-1, 1-\frac{\alpha }{2}} \lt \frac{V_X^2}{V_Y^2} \right\}\]

[演習問題]

一般に，ワイン瓶1本の内容量は750mlである．しかし，KくんはW社の製造するワイン瓶について，内容量が規定の750mlよりも少ないのではないかと疑っている．調査の結果，KくんはW社が製造した100本のワイン瓶を標本として得た．この場合，帰無仮説と対立仮説をどのように設定するのが適切であるか答えよ．また，適切な検定方式について答えよ．