1. 確率

確率とは「ランダムネス（不確実性）の傾向を数学的に記述するもの」であり，統計的推測とは「確率を観測データから推測し知的な確率モデルを構築すること」です．

つまり，統計学は「不確実性を科学するために基本となる数学的な道具を提供」します．

1.1 事象と確率

曖昧な定義

以下の概念を導入する．

• 試行(Trial)：実験・観測・調査などの不確かさを伴う行為
• 事象(Event) \(A\)：起こりうる試行結果の集まり．
• 全事象/標本空間(All events/Sample space) \(\Omega\)：起こりうる事象の集まり

確率\(P(A)\)は，事象\(A\)を区間\([0,1]\)に対応させる関数である．

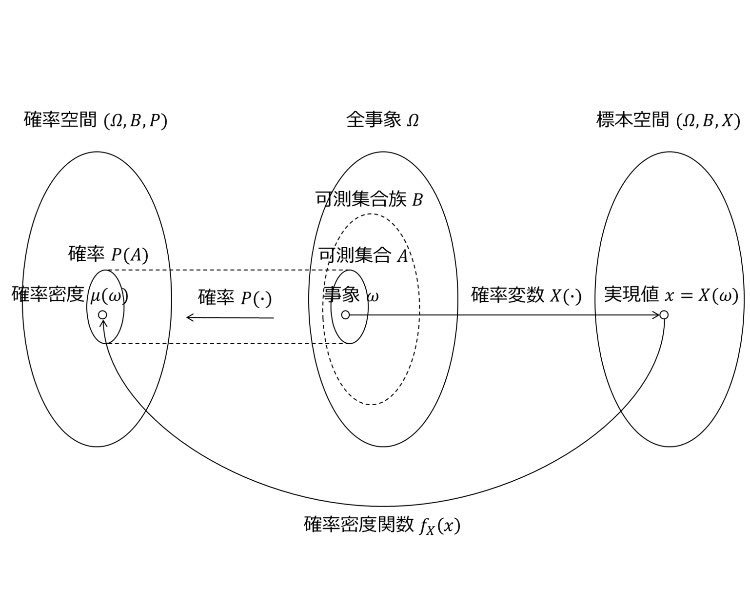
測度論による定義

「確率\(P(A)\)は，事象\(A\) を区間\([0,1]\)に対応させる関数である．」

Q. では事象\(A\)とは何か？（事象\(A\)の数学的な性質は？）

A. 事象\(A\)は可測集合（つまり，可測集合であれば確率\(P(\cdot)\)を考えることができる）

• 可測集合(Measurable set) \(A\)
  • 定義：可測集合族 \(\mathcal{B}\) の元
• 可測集合族(Measurable family) \(\mathcal{B}\)
  • 定義：以下を満たす集合．
    • \(\emptyset \in \mathcal{B}, ~ \Omega \in \mathcal{B}\).
    • \(A \in \mathcal{B} \Rightarrow \overline{A} \in \mathcal{B}\).
    • \(A_k \in \mathcal{B}, ~ (k=1,2,\dots) \Rightarrow \cup_{k=1}^{\infty} A_k \in \mathcal{B}\).

よって，確率\(P(\cdot)\)の測度論による定義は以下のようになる．

※ 確率\(P(\cdot)\)とは，測度\(M(\cdot)\)を正規化(=スケールを[0,1]に揃える)したもの．

• 確率(probability) \(P(\cdot)\)
  • 定義：可測集合\(A\)に対する関数\(P(\cdot)\)で，以下を満たすもの．
    • \(\forall A \in \mathcal{B}, ~ P(A) \gt 0\).
    • \(P(\Omega) = 1\).
    • 互いに排反な集合\(A_k \in \mathcal{B}, ~ (k=1,2,\dots)\) に対して，\(P(\cup_{k=1}^{\infty} A_k) = \sum_{k=1}^{\infty} P(A_k)\) が成り立つ．

1.2 条件つき確率と独立

独立の定義

以下が成り立つとき，「事象\(A\)と事象\(B\)は独立である」という．

\[P(A, B) = P(A)P(B)\]

条件付き確率の定義

2つの事象\(A, B\)に対して，

\[P(A \vert B) = \frac{P(A, B)}{P(B)}\]

を「\(B\)を与えたときの\(A\)の条件つき確率(conditional probability)」という．

全確率の公式(Law of total probability)

互いに排反な事象\(B_1, B_2, \dots, B_n\)に対して，事象\(A\)の確率は以下のように分解できる．

\[P(A) = \sum_{k=1}^{n} P(A \vert B_k)P(B_k)\]

ベイズの定理(Bayes rule)

互いに排反な事象\(B_1, B_2, \dots, B_n\)に用いると，条件付き確率\(P(B_j \vert A)\)は以下のように分解できる．

\[P(B_j \vert A) = \frac{P(A \vert B_j)P(B_j)}{ \sum_{k=1}^{n} P(A \vert B_k)P(B_k)}\]

[演習問題]

ある病気について疾患の有無を調べる簡易的な検査方法がある．この方法によると，疾患がないのに陽性反応が出てしまう確率は20%であり，一方疾患があるのに陰性となる確率は10%である．その病気にかかっているのは全体の10%であるとする．このとき，ある患者に陽性反応が出たとき，その患者が病気にかかっている確率をBayesの定理を使って求めよ.

---