4. 標本分布とその近似

得られたデータから，確率分布の特性値（平均・分散など）に関して推定・検定・信頼区間・予測などの具体的な推測手法を与えて，その推測手法の信頼性を見積もることが統計的推測の目的である．しかし，手元にあるデータ自体は定まった値であり，これをどのように確率分布と関係づけるかが問題となる．そこで，推測統計学では母集団/母分布と標本/標本分布という概念を導入することでこれを解決する．すなわち，母集団/母分布として適当な確率分布や確率モデルを仮定し，標本は母集団/母分布に従う確率変数，観測データは確率変数の実現値と考える．

4.1 統計量と標本分布

統計学は，目的に応じて記述統計と推測統計に分けることができる．

記述統計(Descriptive statistics)
- 目的：データからヒストグラム・箱ひげ図を描いたり，平均・分散などの要約統計量を計算して母集団の特性を調べる
推測統計(Inferential statistics)
- 目的：母集団に確率モデルを想定し，その確率分布に従う確率変数の実現値としてデータをとらえる．

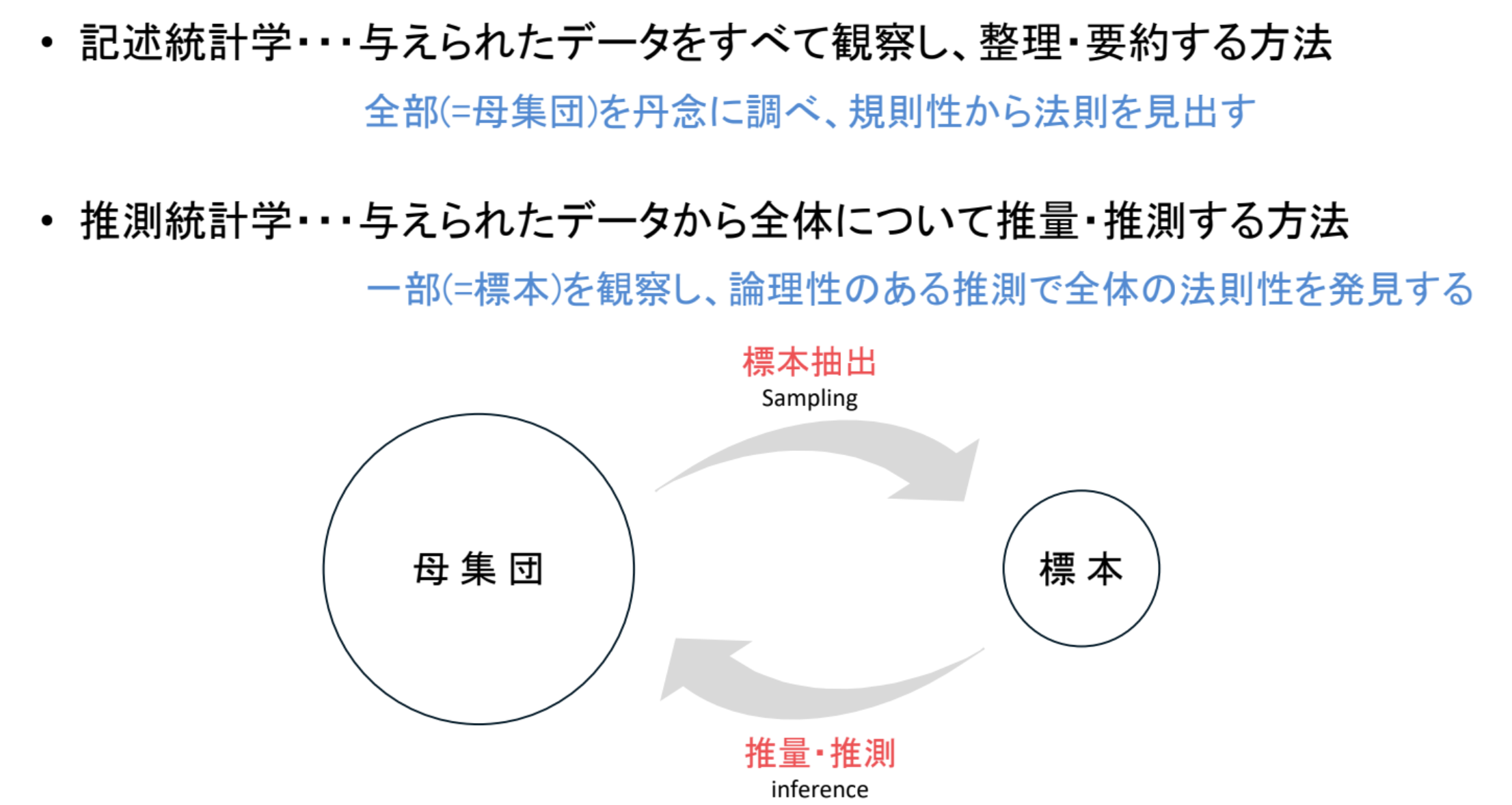
ここで，推測統計を行うための概念的な枠組みとして，母集団/母分布と標本/標本分布を導入する．母集団/母分布と標本/標本分布を理解するために，まず以下の例をみてほしい．

（例1：国勢調査，政権の支持率調査，製品の不良率調査）

これらの統計調査では，母集団が存在するが，母分布は存在しない．

たとえば，政権支持率の値に興味がある場合，母集団(Population)は「有権者全体」になる．このとき，「母集団の要素全てを調査すること＝有権者全員を調査すること」を全数調査(complete survey)という．選挙や国勢調査では全数調査を行う．しかし，コストや速報性の観点から全数調査が現実的ではない場面も多い．そこで，母集団からいくつかの標本(sample)を抽出して，これを基に母集団の推測を行う．

（例2：コインやサイコロの結果予想，株価予測）

これらの推測問題では，母集団が存在しないが，母分布する（と考える）．

たとえば，表が出る確率が$p$で裏が出る確率が$1-p$であるコインの出目に興味がある場合，母分布(Population distribution)はベルヌーイ分布$Ber(p)$となる．このとき，「コインを投げる」という試行は無限に繰り返せるため，全数調査は不可能である．そこで，観測データである「何回かコインを投げた結果」を母分布から抽出された標本(sample)の実現値と考えて，これを基に母集団の推測を行う．

次に推測統計の用語を定義する．

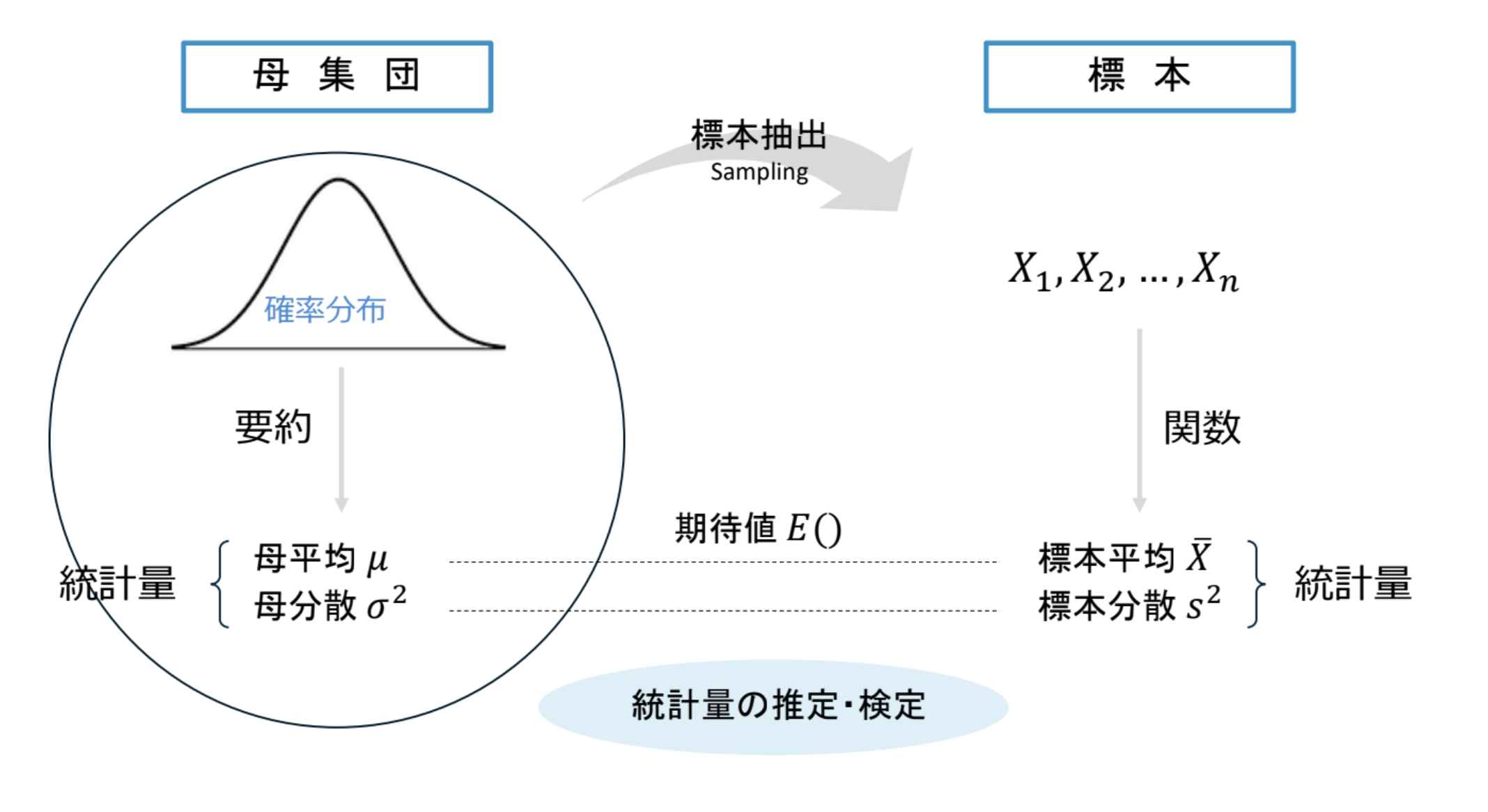
母集団と母分布

母集団(Population) $\Omega$：
- 調査したいすべての対象が含まれる集合
母分布(Population distribution) $p(x)$：
- 推測したい変数$X$の従う真の確率分布

無作為抽出

無作為抽出(Random sampling)：
- 乱数などを用いてランダムに標本を抽出すること．
無作為標本(Random sample)：
- 無作為抽出によって，抽出された標本(データ)．
独立同分布(Independently and identically distribution)
- 確率変数$X_1, \dots, X_n$は互いに独立かつ，各$X_i$が同じ確率分布$P$に従っているとき，「$X_1, \dots, X_n$は互いに独立同分布に従う」といい，以下のように記述する．
  \[X_1, \dots, X_n ~ i.i.d. \sim ~ P\]

標本と標本分布

標本(Sample) $\{ X_1, \dots, X_n \}$：
- 母分布$p(x)$ に従う$n$個の確率変数$X_i ~ (i=1, \dots, n)$．
母数(Population parameter) $\theta$：
- 母分布を決定する定数（パラメータ）や特性値（平均や分散）
  - 母平均$\mu$：母分布$p(x)$の平均
    \[\mu := \int x p(x) dx\]
  - 母分散$\sigma^2$：母分布$p(x)$の分散
    \[\sigma^2 := \int {( x - \mu )}^2 p(x) dx\]
統計量(Statistics) $t(X_1, \dots, X_n)$：
- 標本$\{ X_1, \dots, X_n \}$ に基づいた関数で，母数$\theta$ を含まないもの．
  - 標本平均$\overline{X}$：標本$\{ X_1, \dots, X_n \}$ の平均
    \[\overline{X} := \frac{1}{n} \sum_{i=1}^{n} X_i\]
  - 標本分散$S^2$：標本$\{ X_1, \dots, X_n \}$ の分散
    \[S^2 := \frac{1}{n} \sum_{i=1}^{n} {(X_i - \overline{X})}^2\]
標本分布(Sample distribution) $p(t)$：
- 統計量$t(X_1, \dots, X_n)$の確率分布

代表的な母数

確率変数$X$の母平均$\mu$：母分布$p(x)$の平均
\[\mu := \int x p(x) dx\]
確率変数$X$の母分散$\sigma^2$：母分布$p(x)$の分散
\[\sigma^2 := \int {( x - \mu )}^2 p(x) dx\]

代表的な統計量

以下の統計量（標本）は，

確率変数$X$の標本平均(Sample mean) $\overline{X}$：
\[\overline{X} := \frac{1}{n} \sum_{i=1}^{n} X_i\]
確率変数$X$の標本分散(Sample variance) $S^2$：
\[S^2 := \frac{1}{n} \sum_{i=1}^{n} {(X_i - \overline{X})}^2\]
確率変数$X$の標本不変分散(Sample invariant variance) $V^2$：
\[V^2 := \frac{1}{n-1} \sum_{i=1}^{n} {(X_i - \overline{X})}^2\]
確率変数$X$のt-統計量(t-statistics) $T$：
\[T := \frac{\sqrt{n} (\overline{X} - \mu) }{V}\]
確率変数$X,Y$のF-統計量(F-statistics) $F$：
\[F := \frac{S_X^2}{S_Y^2}\]

4.2 確率変数と確率分布の収束

マルコフの不等式(Markov’s inequality)

非負の確率変数$Y \geq 0$に対して，以下が成り立つ．

\[\forall c \gt 0, ~~~ P(Y \geq 0) \leq \frac{E[Y]}{c}\]

（証明）

$\begin{align} c \cdot P(Y \geq 0) &= c \int_{c}^{\infty} f(y) dy \\ &= \int_{c}^{\infty} c f(y) dy \\ &\leq \int_{c}^{\infty} y f(y) dy \\ &\leq \int_{0}^{\infty} y f(y) dy = E[Y] \end{align}$

チェビシェフの不等式

確率変数$X$とその平均$\mu := E[X]$と分散$\sigma^2 := V[X]$に対して，以下が成り立つ．

\[\forall k \gt 0, ~~~ P( \vert X - \mu \vert \geq k) \leq \frac{\sigma^2}{k^2}\]

（証明）

マルコフの不等式で$Y = {( X - \mu )}^2$，$c = k^2$とおくと，
$\begin{align} \forall k^2 \gt 0, ~~~ &P({(X - \mu)}^2 \geq k^2) \leq \frac{E[{(X - \mu)}^2]}{k^2} \\ \therefore ~~~ &P( \vert X - \mu \vert \geq k) \leq \frac{\sigma^2}{k^2} \end{align}$
となる．

大数の法則

$n$ 個のランダムサンプル$X_1, \dots, X_n ~ i.i.d. \sim ~ (\mu, \sigma^2)$ に対して，以下が成り立つ．

\[\lim_{n \to \infty} \frac{1}{n} \sum_{i=1}^{n} X_i = \mu\]

（証明）

チェビシェフの不等式より，$\forall \varepsilon \gt 0$に対して，
$\begin{align} 0 \leq P(\vert \overline{X} - \mu \vert \geq \varepsilon) &\leq \frac{V[\overline{X}]}{\varepsilon^2} \\ &= \frac{E[{(\overline{X} - \mu)}^2]}{\varepsilon^2} \\ &= \frac{\sigma^2}{n \varepsilon^2} \to 0 ~~~ (n \to \infty) \end{align}$
だから，はさみうちの原理より，
\[\lim_{n \to \infty} P(\vert \overline{X} - \mu \vert \geq \varepsilon) = 0\]
となる．

中心極限定理(Central Limit Theorem, CLT)

$n$ 個のランダムサンプル$X_1, \dots, X_n ~ i.i.d. \sim ~ (\mu, \sigma^2)$ に対して，以下が成り立つ．

\[\lim_{n \to \infty} P \left( \frac{\sqrt{n}(\overline{X} - \mu)}{\sigma} \leq x \right) = \int_{-\infty}^{x} \frac{1}{\sqrt{2 \pi}} e^{- \frac{t^2}{2}} dt\]

すなわち，

\[\overline{X} \underset{~~~d}{\longrightarrow} \mathcal{N} \left( \mu, \frac{\sigma^2}{n} \right)\]

（証明）

略．正規分布の特性関数をTaylor展開して2次近似して，右辺を導出する．

[演習問題]

$X_1, \dots, X_n i.i.d. \sim p_X(x)$とする．このとき，確率変数$X$の平均$E[X]=\mu$ と分散$V[X]=\sigma^2$を用いて，標本平均$\bar{X} := \frac{1}{n} \sum_{i=1}^{n} X_i$ の平均と分散を求めよ．